独立样本 t 检验与相关样本 t 检验

标签

学习/心理学

字数

2167 字

阅读时间

9 分钟

本章概览

在之前的学习中，我们掌握了单样本 t 检验。在本章，我们学习了两样本 t 检验的方法。其中，独立样本 t 检验是在两样本互不相关的基础上进行的，而相关样本t检验的两样本之间存在匹配或前后比较关系。学会区分并应用这两种t检验方法，有助于我们判断两个样本之间是否存在显著差别。注意学习本章时，可以结合之前单样本 t 检验的内容进行对比学习。

学习要点

1. 区分独立样本t检验与相关样本t检验
2. 掌握独立样本t检验与相关样本t检验的逻辑
3. 学会计算独立样本与相关样本的t统计量
4. 学习独立样本t检验与相关样本t检验的统计前提
5. 掌握独立样本t检验与相关样本t检验的效应与效力

独立样本均值差异的分布

在独立样本设计中，每一个总体都有一个均值分布，这样对两个总体来说，我们就要处理两个不同的均值分布。我们从第一个总体的均值分布中随机选择一个均值，再从第二个总体的均值分布中随机选择一个均值。将抽取的两个均值相减，得到一个均值差异的分数，多次重复这一过程，我们就可以得到一个均值差异的分布。

如果虚无假设是正确的，那么两个总体的均值是相等的，所以我们得到的均值差异的分布的均值是0。这一分布的方差总体取决于估计的总体方差，因此我们可以把它看作一个t分布来进行检验。我们先利用样本方差来估计总体方差，从而估计总体样本分布的方差，然后再结合两个样本均值分布的方差构造一个新的估计值，用于描述样本均值分布的变异。

独立样本的 t 统计量

独立样本t检验的假设

• 虚无假设（$H_0$：${\mu }_1-{\mu }_2=0$）：独立样本所来自的两个总体的均值之间没有显著的差异，即所抽取的两个样本来自同一个总体。

• 备择假设（$H_1$：${\mu }_1-{\mu }_2\ne 0$）：独立样本所来自的两个总体的均值之间有显著差异。

总体方差的估计

总体方差的合并估计值为 $S_p^2={\displaystyle \frac{S{S}_1+S{S}_2}{d{f}_1+d{f}_2}}$

• 估计的思路：将两样本进行加权平均，权重是样本的自由度
• 估计的前提：两样本方差大体相等（即满足方差同质性）

均值分布的方差的计算

• $S_1^2={\displaystyle \frac{S_p^2}{n_1}}$

• $S_2^2={\displaystyle \frac{S_p^2}{n_2}}$

• 计算的思路：由于样本容量 $n$ 存在差异，两个样本均值的分布不一定相同，因此均值分布的变异性需要考虑样本容量。

标准误的计算

• $S_{\overline{X_1}-\overline{X_2}}^2=S_1^2+S_2^2$

• $S_{\overline{X_1}-\overline{X_2}}=\sqrt{{\displaystyle \frac{S_p^2}{n_1}}+{\displaystyle \frac{S_p^2}{n_2}}}$

• 计算的思路：均值差异样本的方差是总体1与总体2的均值分布的方差之和。

t 统计量的计算

• $t={\displaystyle \frac{(\overline{X_1}-\overline{X_2})-({\mu }_1-{\mu }_2)}{S_{\overline{X_1}-\overline{X_2}}}}={\displaystyle \frac{(\overline{X_1}-\overline{X_2})}{S_{\overline{X_1}-\overline{X_2}}}}$

与单样本T检验的不同之处

1. 比较的分布是均值差异的分布（$\overline{X_1}-\overline{X_2}$）
2. 确定 t 的临界值是基于两个样本的自由度（$d{f}_1$ 和 $d{f}_2$）
3. 比较分布的样本分数是基于两个分数之差

独立样本t检验的统计前提

1. 观察间彼此独立
2. 两个总体均为正态分布
3. 两个总体具有相等的方差（方差同质性）

一般情况下，独立样本 t 检验对于违反前提条件的情况有一定的耐受性。当使用双尾检验或当样本量不是很小时，t 检验都是很稳健（robust）的。如果因为某些原因我们觉得总体可能不是正态分布，那么应该尽量选用相对较大的样本。

• 方差同质性（homogeneity of variance），也称方差齐性，即要比较两个总体是否具有相同的方差。t 统计量公式中的联合方差是对两个样本方差进行平均以后得到的，而这样的操作只有当这两个值用来估计同一总体的方差时才有意义。

• Hartley最大F值检验（Hartley's Fmax test）,检验方差是否同质的方法。Fmax为两方差的比值，把较大的样本方差置于分子，较小的置于分母，这样Fmax的值总是大于1的。

• 拇指原则：对于小样本(n＜10) ，如果一个方差是另一个的四倍以上，则不满足方差齐性；对于大样本，标准为2倍。

独立样本t检验的效应量、置信区间和效力

独立样本 t 检验的效应量

效应量 (effect size, ES) 的大小代表两个总体分布的重叠程度。在独立样本 t 检验中，效应大小的计算公式如下：

$$ES={\displaystyle \frac{\overline{X_1}-\overline{X_2}}{S_p}}$$

其中 $\overline{X_1}$ 和 $\overline{X_2}$ 分别代表两个独立样本的均值，而 $S_p$ 代表的是对总体标准差的估计值。ES越小，代表重叠程度越大，效应越小；ES越大，重叠程度越小，效应越大。

独立样本 t 检验的置信区间

独立样本 t 检验的置信水平为 $1-\alpha$ 的置信区间为：

$$[\bar{X}-\bar{Y}\pm t_{\alpha /2}(n_1+n_2-2)S_w\sqrt{{\displaystyle \frac{1}{n_1}}+{\displaystyle \frac{1}{n_2}}}]$$

其中 $S_w$ 是对总体标准差的估计值。

独立样本 t 检验的效力

效力的大小和显著性水平、样本容量和检验方向有关。

• 样本量越大，效力越高；
• 效应越大，效力越高；
• 相同条件下单尾检验的效力比双尾检验效力高。、

相关样本 t 检验统计量

相关样本的意义

• 被试内设计，两组数据不存在组间差异。
• 匹配组t-test是有一个或若干个特征使得被试内两两建立联系，这种联系时实验前建立的，分析数据时已匹配成对。
• 匹配能大大减少个体间的误差，提高统计效力。

相关样本 t 检验的逻辑

• 相关样本 t 统计量的计算基于样本分数的差异，每一对对应数据的差异 D 构成了一个差异样本
• 平均数$D=X_1-X_2$
• 方差$S^2={\displaystyle \frac{S{S}_D}{df}}={\displaystyle \frac{\sum D^2-{\displaystyle \frac{(\sum D{)}^2}{n}}}{df}}$

相关样本 t 的计算

• $S_{\bar{D}}=\sqrt{{\displaystyle \frac{S^2}{n}}}$
• $t={\displaystyle \frac{\bar{D}-{\mu }_D}{S_{\bar{D}}}}$

相关样本 t 检验的效应大小

• 效应大小=差异样本均值/差异样本方差

相关样本t检验的效应量、置信区间和效力

相关样本t检验的效应量

• 效应量（effect size）：表示两个分布的重叠程度，它反映研究中处理效应的大小。效应量不受样本量影响。
• 相关样本 t 检验的效应量＝差异样本均值/差异样本方差，即

$$\text{Cohen’s}d=ES={\displaystyle \frac{\bar{D}}{S_D}}$$

相关样本 t 检验的置信区间

两个相关样本差异的95%置信区间为：

$$(\bar{D}-t_{(\alpha /2,df)}{S}_{\bar{D}},\bar{D}+t_{(\alpha /2,df)}{S}_{\bar{D}})$$

相关样本t检验的效力

研究结果的统计效力、效应大小、样本容量以及显著性水平相互联系。当显著性水平为0.05时，统计效力与效力大小、样本容量的关系如表所示。

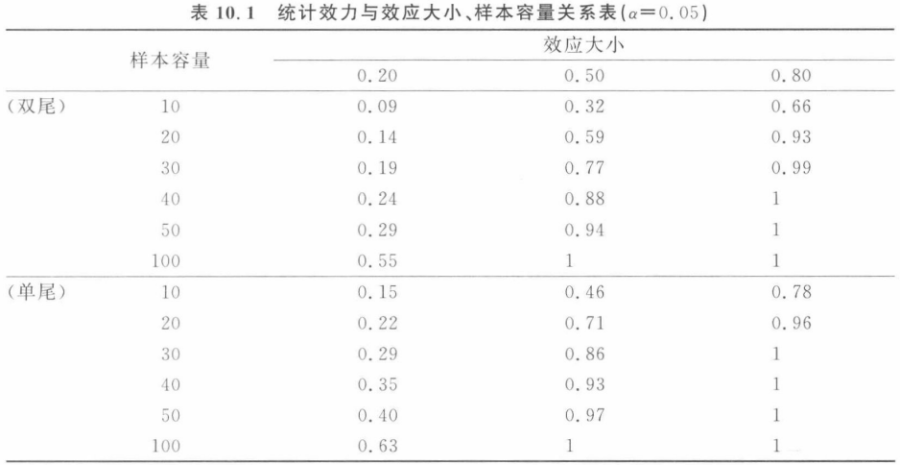
相关样本 t 检验的统计前提

• 在每一种处理条件内，观察都彼此独立
• 差异分数的总体分布是正态的
• 不需要考虑方差同质性

贡献者

芷沐沐

页面历史

最后编辑于 超过 1 年前

查看完整历史

7d09a64-fix

6e41bed-fix

4d369d5-update and test

069049e-update

93be6fb-update

9dc9d35-update